Kybernetika a sociologie (MSgS): Porovnání verzí
m (doopravena matematická sazba) |
(Přidána poslední věta Viz též heslo sociologie kybernetická ve Velkém sociologickém slovníku (1996)) |
||
| (Není zobrazena jedna mezilehlá verze od jednoho dalšího uživatele.) | |||
| Řádek 8: | Řádek 8: | ||
Ad 1.: Vysvětlíme nejprve na příkladech význam výroku „Model <math>M</math> přísluší originálu <math>O</math>“ nebo, což je totéž, „<math>M</math> je modelem originálu <math>O</math>“. Předpokládejme, že průměrná doba sledování televize ve všední den v určité populaci (např. členové rodin vlastnících televizor v určité geografické oblasti) odpovídá obr. 1, kde body značí vyšetřené hodnoty | Ad 1.: Vysvětlíme nejprve na příkladech význam výroku „Model <math>M</math> přísluší originálu <math>O</math>“ nebo, což je totéž, „<math>M</math> je modelem originálu <math>O</math>“. Předpokládejme, že průměrná doba sledování televize ve všední den v určité populaci (např. členové rodin vlastnících televizor v určité geografické oblasti) odpovídá obr. 1, kde body značí vyšetřené hodnoty | ||
| − | + | [[Soubor:MSgS_kybernetika-a-sociologie_1.JPG|frameless|900px]] | |
a kde vysílání pro sledovanou oblast bylo zahájeno začátkem března. Tento jev bude pro nás originálem. Představme si dále elektronické zařízení podle obr. 2, které má dvě svorky <math>A</math>, <math>A'</math> vlevo a dvě svorky <math>B</math>, <math>B'</math> vpravo. Jestliže náhle zavedeme konstantní napětí na svorky <math>A</math>, <math>A'</math>, bude se napětí na svorkách <math>B</math>, <math>B'</math> měnit podle grafu na obr. 3. (O konstrukci takového přístroje, jež je poměrně jednoduchá, není zde nutno uvažovat.) Je patrné, že časový průběh napětí <math>U</math> (ve voltech) na přístroji odpovídá době sledování 5 (v hodinách denně) na originálu podle modelové rovnice | a kde vysílání pro sledovanou oblast bylo zahájeno začátkem března. Tento jev bude pro nás originálem. Představme si dále elektronické zařízení podle obr. 2, které má dvě svorky <math>A</math>, <math>A'</math> vlevo a dvě svorky <math>B</math>, <math>B'</math> vpravo. Jestliže náhle zavedeme konstantní napětí na svorky <math>A</math>, <math>A'</math>, bude se napětí na svorkách <math>B</math>, <math>B'</math> měnit podle grafu na obr. 3. (O konstrukci takového přístroje, jež je poměrně jednoduchá, není zde nutno uvažovat.) Je patrné, že časový průběh napětí <math>U</math> (ve voltech) na přístroji odpovídá době sledování 5 (v hodinách denně) na originálu podle modelové rovnice | ||
| Řádek 20: | Řádek 20: | ||
kde se doba <math>T</math> počítá od zahájení vysílání a doba <math>t</math> od přivedení napětí na svorky <math>A</math>, <math>A'</math>. | kde se doba <math>T</math> počítá od zahájení vysílání a doba <math>t</math> od přivedení napětí na svorky <math>A</math>, <math>A'</math>. | ||
| − | + | [[Soubor:MSgS_kybernetika-a-sociologie_2.JPG|frameless|900px]] | |
Protože popsaný přístroj umožňuje (pomocí modelových rovnic) výhodně analyzovat jev, sledovaný na originále, lze jej považovat za model (a to takzvaný analogový model čili analogon) a s jeho pomocí např. odhadnout dobu <math>S</math> v obdobích, kde nebyla měřena. Tak např. průměrná doba sledování <math>S</math> na začátku září, tj. v době <math>T = 6</math> měsíců od začátku vysílání, bude odpovídat podle obr. 3 údaji pro <math>t = 6</math> sec. na modelu, tedy hodnotě <math>U = 12</math> V. Podle modelové rovnice odhadneme z toho dobu sledování <math>S = 1,2</math> hodiny denně. | Protože popsaný přístroj umožňuje (pomocí modelových rovnic) výhodně analyzovat jev, sledovaný na originále, lze jej považovat za model (a to takzvaný analogový model čili analogon) a s jeho pomocí např. odhadnout dobu <math>S</math> v obdobích, kde nebyla měřena. Tak např. průměrná doba sledování <math>S</math> na začátku září, tj. v době <math>T = 6</math> měsíců od začátku vysílání, bude odpovídat podle obr. 3 údaji pro <math>t = 6</math> sec. na modelu, tedy hodnotě <math>U = 12</math> V. Podle modelové rovnice odhadneme z toho dobu sledování <math>S = 1,2</math> hodiny denně. | ||
| Řádek 41: | Řádek 41: | ||
Symbolicky lze rovnici (*) popsat tzv. blokovým schématem podle obr. 4, na němž je patrná vstupní informace, tj. doba <math>T</math>, která uplynula od začátku vysílání; blok, který na podkladě vstupní informace vytváří informaci výstupní; a výstupní informace, tj. doba <math>S</math>. Blokové schéma na obr. 4 neříká o sledovaném originálu nic více než sama rovnice (*); pro složité soustavy bývá však blokové schéma přehlednější. U složitých soustav vytvářejí se často i modely statické, modelující originál pro jeden určený časový okamžik, na rozdíl od dosud popsaných modelů dynamických, modelujících časový průběh jevů. | Symbolicky lze rovnici (*) popsat tzv. blokovým schématem podle obr. 4, na němž je patrná vstupní informace, tj. doba <math>T</math>, která uplynula od začátku vysílání; blok, který na podkladě vstupní informace vytváří informaci výstupní; a výstupní informace, tj. doba <math>S</math>. Blokové schéma na obr. 4 neříká o sledovaném originálu nic více než sama rovnice (*); pro složité soustavy bývá však blokové schéma přehlednější. U složitých soustav vytvářejí se často i modely statické, modelující originál pro jeden určený časový okamžik, na rozdíl od dosud popsaných modelů dynamických, modelujících časový průběh jevů. | ||
| − | + | [[Soubor:MSgS_kybernetika-a-sociologie_3.JPG|frameless|900px]] | |
Dosud popsané modely byly modely kvantitativní, tj. zobrazovaly (v určitém měřítku) kvantitativní znak, odpovídající sledovanému jevu na originále. Návrh i užití kvantitativního modelu vyžaduje respektování řady zásad. Jejich porušení vede k výsledkům, které se laikovi mohou zdát přesné a vědecké, zatímco hrubě zkreslují skutečnost. Hlavní obtíží je okolnost, že v sociologii není dosud lehké získat dostatek údajů o sledované populaci, podle kterých lze model sestavit, a že bývá obtížné rozhodovat, zda model, odvozený v určité době na určitém místě, platí i pro jinou dobu a jiné místo (problém oprávněnosti predikce, problém stacionárnosti jevů, problém homogenity univerza sledování). Proto kvantitativní modely nabyly největšího významu v přírodních vědách a technice a začínají se uplatňovat v ekonomice, medicíně, psychologii apod. Jejich aplikace v sociologii je závislá především na tom, kdy sociologický výzkum dokáže vyšetřit dostatečné množství validních informací. | Dosud popsané modely byly modely kvantitativní, tj. zobrazovaly (v určitém měřítku) kvantitativní znak, odpovídající sledovanému jevu na originále. Návrh i užití kvantitativního modelu vyžaduje respektování řady zásad. Jejich porušení vede k výsledkům, které se laikovi mohou zdát přesné a vědecké, zatímco hrubě zkreslují skutečnost. Hlavní obtíží je okolnost, že v sociologii není dosud lehké získat dostatek údajů o sledované populaci, podle kterých lze model sestavit, a že bývá obtížné rozhodovat, zda model, odvozený v určité době na určitém místě, platí i pro jinou dobu a jiné místo (problém oprávněnosti predikce, problém stacionárnosti jevů, problém homogenity univerza sledování). Proto kvantitativní modely nabyly největšího významu v přírodních vědách a technice a začínají se uplatňovat v ekonomice, medicíně, psychologii apod. Jejich aplikace v sociologii je závislá především na tom, kdy sociologický výzkum dokáže vyšetřit dostatečné množství validních informací. | ||
| Řádek 47: | Řádek 47: | ||
V mnohých případech je pro názornost vhodné sestavit modely kvalitativní. Podávají názorný přehled, mezi kterými jevy se souvislosti sledují, aniž by intenzitu nebo formu souvislostí číselně vyjadřovaly. Lze jich tedy užít i pro znaky kvalitativní nebo pro znaky kvantitativní, jejichž hodnoty a souvislosti dosud neznáme. Tak místo blokového schématu na obr. 4 lze navrhnout blokové schéma na obr. 5, které odpovídá výroku: „Průměrná doba sledování S závisí na době, která uplynula od zahájení vysílání, a na kalendářním datu“ (tj. respektuje např. větší zájem o vysílání v zimních měsících). Tento výrok lze jinak vyjádřit slovy „Při úvaze o průměrné době sledování zanedbáváme všechny vlivy kromě dvou uvedených vstupních informací“. Modelem sledovaného jevu je tedy uvedený (velmi jednoduchý) systém. | V mnohých případech je pro názornost vhodné sestavit modely kvalitativní. Podávají názorný přehled, mezi kterými jevy se souvislosti sledují, aniž by intenzitu nebo formu souvislostí číselně vyjadřovaly. Lze jich tedy užít i pro znaky kvalitativní nebo pro znaky kvantitativní, jejichž hodnoty a souvislosti dosud neznáme. Tak místo blokového schématu na obr. 4 lze navrhnout blokové schéma na obr. 5, které odpovídá výroku: „Průměrná doba sledování S závisí na době, která uplynula od zahájení vysílání, a na kalendářním datu“ (tj. respektuje např. větší zájem o vysílání v zimních měsících). Tento výrok lze jinak vyjádřit slovy „Při úvaze o průměrné době sledování zanedbáváme všechny vlivy kromě dvou uvedených vstupních informací“. Modelem sledovaného jevu je tedy uvedený (velmi jednoduchý) systém. | ||
| − | + | [[Soubor:MSgS_kybernetika-a-sociologie_4.JPG|frameless|800px]] | |
Kvalitativní modely mají význam zejména pro systémy složité. V širším slova smyslu považujeme za model i popis jevů v určité populaci, který určuje hlavní souvislosti (viz [[model a modelování v sociologii (MSgS)|model a modelování v sociologii]]). | Kvalitativní modely mají význam zejména pro systémy složité. V širším slova smyslu považujeme za model i popis jevů v určité populaci, který určuje hlavní souvislosti (viz [[model a modelování v sociologii (MSgS)|model a modelování v sociologii]]). | ||
| Řádek 59: | Řádek 59: | ||
Ad 3.: Užití teoretických základů kybernetiky pro matematické zpracování sociologických problémů je dosud v počátcích. Výsledky, pokud se dostaví, mohou se jevit ve formě obohacení statistických technik. | Ad 3.: Užití teoretických základů kybernetiky pro matematické zpracování sociologických problémů je dosud v počátcích. Výsledky, pokud se dostaví, mohou se jevit ve formě obohacení statistických technik. | ||
| − | Ad 4.: Kybernetika urychlila rozvoj mnoha oborů lidské činnosti, které mohou mít pro sociologii význam. Nejdůležitější z nich je stavba samočinných počítačů a metodika jejich nasazení. | + | Ad 4.: Kybernetika urychlila rozvoj mnoha oborů lidské činnosti, které mohou mít pro sociologii význam. Nejdůležitější z nich je stavba samočinných počítačů a metodika jejich nasazení. |
<span class="section_title">Literatura:</span> <span class="creator">Arab-Ogly E. A.</span>, Sociologia i kibernětika, Voprosy filosofii, 5, 1958; <span class="creator">Arrow K.</span>, Mathematical Models in the Social Science, Stratford, 1951; <span class="creator">George H. P.</span>, Automation, Cybernetics and Society, New York, 1959; <span class="creator">Mac Rae D. G.</span>, Cybernetics and its Relevance to Social Science, British J. of Sociology, June, 1951; <span class="creator">Maslov V. N.</span>, Modělizovanie v sociologičeskich issledovanijach, Voprosy filosofii, 3, 1962; <span class="creator">Simon H. A.</span>, Models of Man Social and Rational, Chapman and Hall, London, 1957; <span class="creator">Smith O. J.</span>, Feedback Control Systems, New York, Mc-Graw Hill, 1958; <span class="creator">Soest J. L.</span>, A Contribution of Information Theory to Sociology Synthese 1954, str. 263; <span class="creator">Wiener N.</span>, Kybernetika a společnost, Praha, 1963; <span class="creator">Wiener N.</span>, Kybernetika, Praha, 1960; <span class="creator">Wiener N.</span>, Kybernetika ve společenských vědách, Mezinárodní sborník statí, Praha, 1965. | <span class="section_title">Literatura:</span> <span class="creator">Arab-Ogly E. A.</span>, Sociologia i kibernětika, Voprosy filosofii, 5, 1958; <span class="creator">Arrow K.</span>, Mathematical Models in the Social Science, Stratford, 1951; <span class="creator">George H. P.</span>, Automation, Cybernetics and Society, New York, 1959; <span class="creator">Mac Rae D. G.</span>, Cybernetics and its Relevance to Social Science, British J. of Sociology, June, 1951; <span class="creator">Maslov V. N.</span>, Modělizovanie v sociologičeskich issledovanijach, Voprosy filosofii, 3, 1962; <span class="creator">Simon H. A.</span>, Models of Man Social and Rational, Chapman and Hall, London, 1957; <span class="creator">Smith O. J.</span>, Feedback Control Systems, New York, Mc-Graw Hill, 1958; <span class="creator">Soest J. L.</span>, A Contribution of Information Theory to Sociology Synthese 1954, str. 263; <span class="creator">Wiener N.</span>, Kybernetika a společnost, Praha, 1963; <span class="creator">Wiener N.</span>, Kybernetika, Praha, 1960; <span class="creator">Wiener N.</span>, Kybernetika ve společenských vědách, Mezinárodní sborník statí, Praha, 1965. | ||
| Řádek 65: | Řádek 65: | ||
''[[:Kategorie:Aut: Pergler Přemysl|Přemysl Pergler]]''<br /> | ''[[:Kategorie:Aut: Pergler Přemysl|Přemysl Pergler]]''<br /> | ||
[[Kategorie:Aut: Pergler Přemysl]] | [[Kategorie:Aut: Pergler Přemysl]] | ||
| + | ---- | ||
| + | <span class="see-also">Viz též heslo [[sociologie kybernetická]] ve [[VSgS|Velkém sociologickém slovníku (1996)]]</span> | ||
[[Kategorie:MSgS]] | [[Kategorie:MSgS]] | ||
Aktuální verze z 10. 11. 2018, 19:18
kybernetika a sociologie (MSgS). Kybernetika je věda o sdělování a řízení v živých organismech a technických systémech (Wiener). Její užití v sociologii, jež je teprve v začátcích, lze zhruba rozdělit na čtyři oblasti:
- Modelování společnosti, tj. vytváření kvalitativních nebo kvantitativních modelů společnosti, sociologických jevů a jejich souvislostí a užití takových modelů k řešení sociologických problémů.
- Analýza toku informace v sociologickém výzkumu a užití této analýzy k verifikaci a ekonomické optimalizaci konkrétních úkolů sociologického výzkumu.
- Analýza údajů při kvantitativních akcích sociologického výzkumu pomocí teorie informací (jež je matematickou disciplinou, související s kybernetikou).
- Užití výsledků jiných odvětví lidské činnosti, které samy kybernetiky využívají.
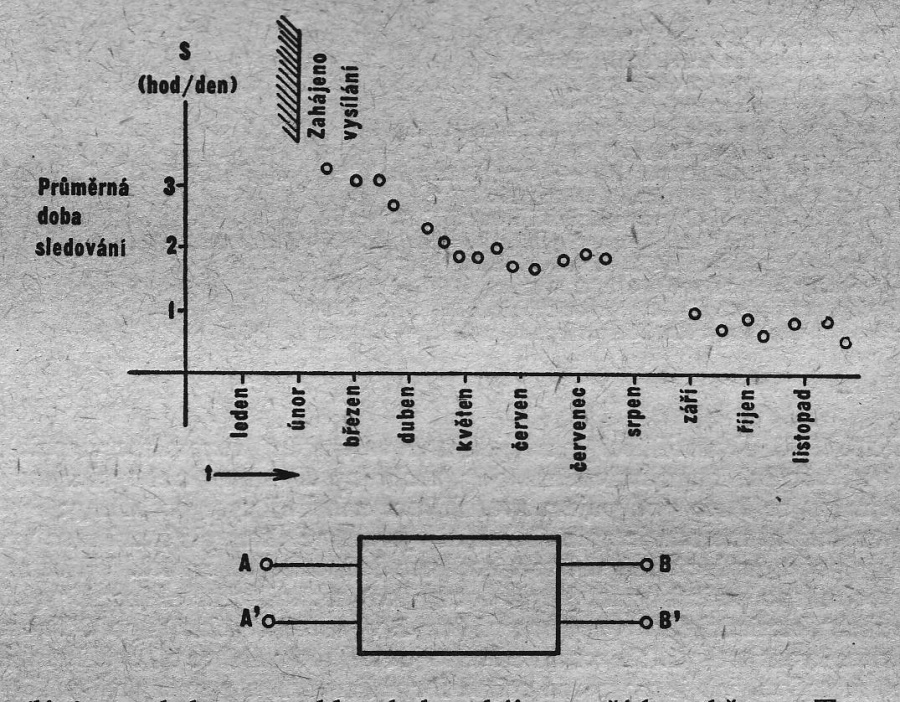
Ad 1.: Vysvětlíme nejprve na příkladech význam výroku „Model [math]M[/math] přísluší originálu [math]O[/math]“ nebo, což je totéž, „[math]M[/math] je modelem originálu [math]O[/math]“. Předpokládejme, že průměrná doba sledování televize ve všední den v určité populaci (např. členové rodin vlastnících televizor v určité geografické oblasti) odpovídá obr. 1, kde body značí vyšetřené hodnoty
a kde vysílání pro sledovanou oblast bylo zahájeno začátkem března. Tento jev bude pro nás originálem. Představme si dále elektronické zařízení podle obr. 2, které má dvě svorky [math]A[/math], [math]A'[/math] vlevo a dvě svorky [math]B[/math], [math]B'[/math] vpravo. Jestliže náhle zavedeme konstantní napětí na svorky [math]A[/math], [math]A'[/math], bude se napětí na svorkách [math]B[/math], [math]B'[/math] měnit podle grafu na obr. 3. (O konstrukci takového přístroje, jež je poměrně jednoduchá, není zde nutno uvažovat.) Je patrné, že časový průběh napětí [math]U[/math] (ve voltech) na přístroji odpovídá době sledování 5 (v hodinách denně) na originálu podle modelové rovnice
[math]S = \frac{U}{10}[/math]
a čas [math]t[/math] (ve vteřinách) na přístroji odpovídá času [math]T[/math] (v měsících) na originále podle sledované rovnice
[math]T = t[/math]
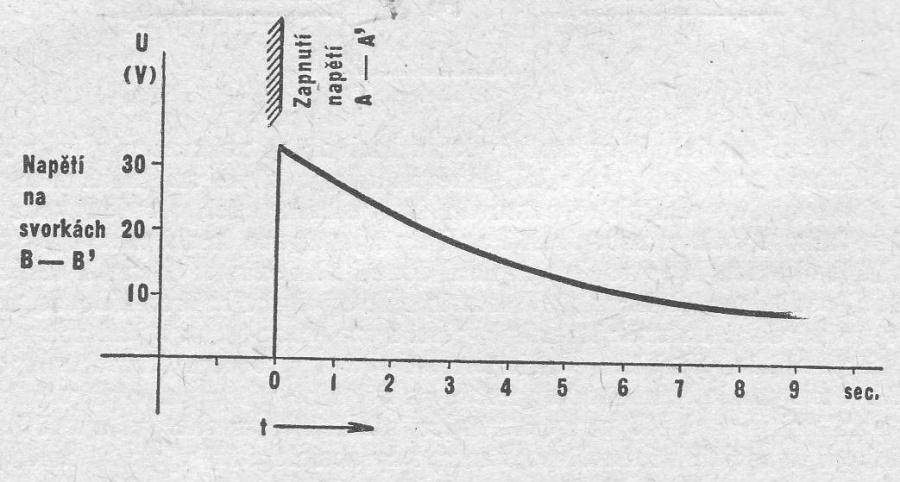
kde se doba [math]T[/math] počítá od zahájení vysílání a doba [math]t[/math] od přivedení napětí na svorky [math]A[/math], [math]A'[/math].
Protože popsaný přístroj umožňuje (pomocí modelových rovnic) výhodně analyzovat jev, sledovaný na originále, lze jej považovat za model (a to takzvaný analogový model čili analogon) a s jeho pomocí např. odhadnout dobu [math]S[/math] v obdobích, kde nebyla měřena. Tak např. průměrná doba sledování [math]S[/math] na začátku září, tj. v době [math]T = 6[/math] měsíců od začátku vysílání, bude odpovídat podle obr. 3 údaji pro [math]t = 6[/math] sec. na modelu, tedy hodnotě [math]U = 12[/math] V. Podle modelové rovnice odhadneme z toho dobu sledování [math]S = 1,2[/math] hodiny denně.
Pro uvedený jednoduchý případ by nebyla stavba analogového modelu účelná. Je-li však nutno sledovat velmi složité souvislosti (a zejména, je-li k dispozici tzv. univerzální analogon, na kterém lze po jednoduchých úpravách řešit mnoho různorodých úloh), může být analogové modelování cennou pomůckou.
V mnohých případech stačí popsat sledovaný jev matematicky.
Tak křivku na obr. 3 lze popsat rovnicí
[math]S = 10 + 20.10 - 0,15 T[/math] pro [math]T \gt 0[/math].
I tuto rovnici (právě tak jako samotný graf na obr. 3) lze považovat za model sledovaného jevu, pokud se pojem „model“ chápe v širokém slova smyslu. Z tohoto hlediska považujeme za model i popis určitého jevu pomocí statistických pojmů, např. „u sledovaného jevu předpokládáme normální rozdělení s aritmetickým průměrem [math]M[/math] a směrodatnou odchylkou [math]S[/math]“.
Je-li originál popsán velmi složitou soustavou rovnic, lze k jejich řešení užít číslicových počítačů. O nich lze říci, že modelují výpočtový postup (tzv. algoritmus), zatímco analogony modelují přímo jev vyšetřovaný na originálu.
Algoritmus pro výpočet doby sledování [math]S[/math] by číslicový počítač řešil sledem kroků tohoto druhu:
- Dobu [math]T[/math] násob číslem 0,69
- Výsledek odečti od čísla 3 atd.... až konečně by vytiskl požadovanou hodnotu [math]S[/math] (odvození tohoto algoritmu zde neuvádíme).
Symbolicky lze rovnici (*) popsat tzv. blokovým schématem podle obr. 4, na němž je patrná vstupní informace, tj. doba [math]T[/math], která uplynula od začátku vysílání; blok, který na podkladě vstupní informace vytváří informaci výstupní; a výstupní informace, tj. doba [math]S[/math]. Blokové schéma na obr. 4 neříká o sledovaném originálu nic více než sama rovnice (*); pro složité soustavy bývá však blokové schéma přehlednější. U složitých soustav vytvářejí se často i modely statické, modelující originál pro jeden určený časový okamžik, na rozdíl od dosud popsaných modelů dynamických, modelujících časový průběh jevů.
Dosud popsané modely byly modely kvantitativní, tj. zobrazovaly (v určitém měřítku) kvantitativní znak, odpovídající sledovanému jevu na originále. Návrh i užití kvantitativního modelu vyžaduje respektování řady zásad. Jejich porušení vede k výsledkům, které se laikovi mohou zdát přesné a vědecké, zatímco hrubě zkreslují skutečnost. Hlavní obtíží je okolnost, že v sociologii není dosud lehké získat dostatek údajů o sledované populaci, podle kterých lze model sestavit, a že bývá obtížné rozhodovat, zda model, odvozený v určité době na určitém místě, platí i pro jinou dobu a jiné místo (problém oprávněnosti predikce, problém stacionárnosti jevů, problém homogenity univerza sledování). Proto kvantitativní modely nabyly největšího významu v přírodních vědách a technice a začínají se uplatňovat v ekonomice, medicíně, psychologii apod. Jejich aplikace v sociologii je závislá především na tom, kdy sociologický výzkum dokáže vyšetřit dostatečné množství validních informací.
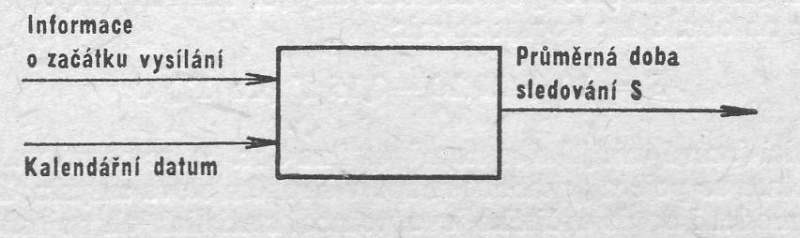
V mnohých případech je pro názornost vhodné sestavit modely kvalitativní. Podávají názorný přehled, mezi kterými jevy se souvislosti sledují, aniž by intenzitu nebo formu souvislostí číselně vyjadřovaly. Lze jich tedy užít i pro znaky kvalitativní nebo pro znaky kvantitativní, jejichž hodnoty a souvislosti dosud neznáme. Tak místo blokového schématu na obr. 4 lze navrhnout blokové schéma na obr. 5, které odpovídá výroku: „Průměrná doba sledování S závisí na době, která uplynula od zahájení vysílání, a na kalendářním datu“ (tj. respektuje např. větší zájem o vysílání v zimních měsících). Tento výrok lze jinak vyjádřit slovy „Při úvaze o průměrné době sledování zanedbáváme všechny vlivy kromě dvou uvedených vstupních informací“. Modelem sledovaného jevu je tedy uvedený (velmi jednoduchý) systém.
Kvalitativní modely mají význam zejména pro systémy složité. V širším slova smyslu považujeme za model i popis jevů v určité populaci, který určuje hlavní souvislosti (viz model a modelování v sociologii).
Modelování sociologického problému se skládá z těchto kroků: a) popis sledovaných jevů v dané populaci pomocí jednoznačně definovaných termínů; b) výběr souvislostí, které se mají respektovat, a předběžné prověření, jaký vliv bude mít zanedbání souvislostí ostatních; c) popis vybraných souvislostí ve formě logické (nebo matematické); d) výběr vhodného typu modelu a návrh jeho struktury; e) zavedení (do modelu) vstupních informací, získaných transformováním informací v originále, tj. o sledovaných sociologických jevech v dané populaci; f) transformace výstupních informací modelu na informace o originále.
Ad 2.: Poznávací řetězec při sociologickém výzkumu lze rozdělit do jednotlivých operací, které jsou charakterizovány zejména popisem vstupních a výstupních informací. (Tak např. vstupní informací operace „třídění“ jsou znaky, tj. údaje o jednotlivých jedincích. Výstupní informací jsou absolutní četnosti.) Každá operace se realizuje některou z technik. (Tak např. třídění lze provést ručně, na děrnoštítkovém stroji apod.)
Lze vybrat omezené množství technik sběru informací v terénu (např. rozhovor, dotazník), statistických technik (např. analýza rozptylu) a dalších technik (viz metody, procedury a techniky). Pomocí těchto technik lze řešit převážnou většinu výzkumných úkolů, které v praxi přicházejí. Jednotlivé operace je účelné chápat jako transformace určité informace a z toho hlediska je sledovat. Vzniká tak poznávací řetězec, začínající prvotním záznamem (např. souborem vyplněných dotazníků) a končící vyhodnocenou informací o populaci (např. konstatováním, jak souvisí fluktuace pracovníků určitého podniku se mzdou, ubytováním, pracovním prostředím atd.). Při užití se pak schéma řetězce dále rozpracovává. Jeho užití může přinést výhody a) až c): a) důsledné sledování toku informace umožňuje systematickou kontrolu validity a ekonomie celého poznávacího řetězce (nelze tak dosáhnout principiálně jiných výsledků než obvyklými validizačními postupy, nýbrž poněkud zmenšit pravděpodobnost, že obvyklé validizační postupy nebudou vhodně nasazeny); b) výklad funkce poznávacího řetězce v sociologii (zejména otázek gnoseologických, problémů validity a měření souvislostí) je podle modelu dobře pochopitelný; c) sledování návazností operací a jejich vstupních a výstupních informací umožňuje vybrat vysoce formalizované operace a rozhodnout, do jaké míry je účelná automatizace jejich provedení.
Ad 3.: Užití teoretických základů kybernetiky pro matematické zpracování sociologických problémů je dosud v počátcích. Výsledky, pokud se dostaví, mohou se jevit ve formě obohacení statistických technik.
Ad 4.: Kybernetika urychlila rozvoj mnoha oborů lidské činnosti, které mohou mít pro sociologii význam. Nejdůležitější z nich je stavba samočinných počítačů a metodika jejich nasazení.
Literatura: Arab-Ogly E. A., Sociologia i kibernětika, Voprosy filosofii, 5, 1958; Arrow K., Mathematical Models in the Social Science, Stratford, 1951; George H. P., Automation, Cybernetics and Society, New York, 1959; Mac Rae D. G., Cybernetics and its Relevance to Social Science, British J. of Sociology, June, 1951; Maslov V. N., Modělizovanie v sociologičeskich issledovanijach, Voprosy filosofii, 3, 1962; Simon H. A., Models of Man Social and Rational, Chapman and Hall, London, 1957; Smith O. J., Feedback Control Systems, New York, Mc-Graw Hill, 1958; Soest J. L., A Contribution of Information Theory to Sociology Synthese 1954, str. 263; Wiener N., Kybernetika a společnost, Praha, 1963; Wiener N., Kybernetika, Praha, 1960; Wiener N., Kybernetika ve společenských vědách, Mezinárodní sborník statí, Praha, 1965.
Viz též heslo sociologie kybernetická ve Velkém sociologickém slovníku (1996)